/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Oblicz długość

Zadanie nr 1418803

Z punktu leżącego na okręgu o promieniu 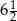1 62 poprowadzono dwie prostopadłe cięciwy. Różnica ich długości jest równa 7. Oblicz długości tych cięciw.

Wersja PDF

Rozwiązanie

Niech 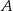A będzie punktem z którego zostały poprowadzone cięciwy 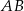AB i AC .

PIC

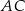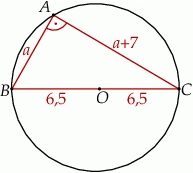
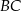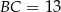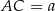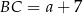Ponieważ cięciwy są prostopadłe, odcinek BC jest średnicą okręgu i BC = 13 . Oznaczmy AC = a i BC = a + 7 . Piszemy teraz twierdzenie Pitagorasa w trójkącie ABC .

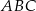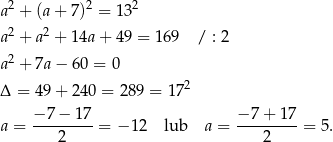
a2 + (a+ 7)2 = 132 2 2 a + a + 14a + 49 = 1 69 / : 2 a2 + 7a − 60 = 0 Δ = 49 + 240 = 2 89 = 172 −7 − 1 7 − 7+ 17 a = ---------= − 12 lub a = ---------= 5. 2 2

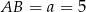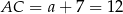Ujemne rozwiązanie odrzucamy i mamy AB = a = 5 . Stąd AC = a + 7 = 1 2 .  
Odpowiedź: 5 i 12

Wersja PDF