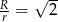/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Oblicz długość

Zadanie nr 2470454

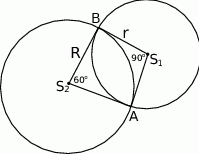
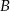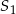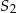Dwa okręgi o środkach S1 i S2 przecinają się w punktach A i B , przy czym punkty S1 i S2 leżą po przeciwnych stronach prostej AB .

PIC

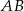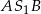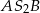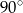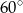Miary kątów AS 1B i AS 2B wynoszą odpowiednio 90 ∘ i 60∘ . Wyznacz stosunek 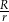Rr- długości promieni tych okręgów.

Wersja PDF

Rozwiązanie

Ponieważ trójkąt 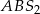ABS 2 jest równoramienny i kąt między ramionami ma miarę 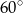60 ∘ , więc jest to trójkąt równoboczny. Zatem AB = R .

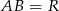Z drugiej strony, trójkąt 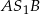AS 1B jest połówką kwadratu, więc 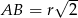√ -- AB = r 2 . Mamy więc

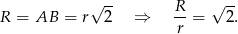
√ -- R- √ -- R = AB = r 2 ⇒ r = 2.

 
Odpowiedź: R-= √ 2- r

Wersja PDF