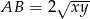/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Oblicz długość

Zadanie nr 3431006

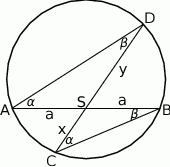
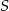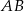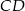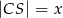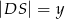Przez środek S cięciwy AB okręgu poprowadzono cięciwę CD , przy czym |CS | = x i |DS | = y . Oblicz długość cięciwy AB .

Wersja PDF

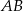Rozwiązanie

Oznaczmy 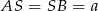AS = SB = a .

PIC

Sposób I

Korzystamy z twierdzenia o siecznych okręgu.

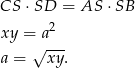
CS ⋅SD = AS ⋅SB xy = a2 √ --- a = xy.

Zatem 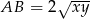√ --- AB = 2 xy .

Sposób II

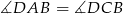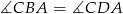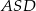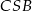Zauważmy, że ∡DAB = ∡DCB i ∡CBA = ∡CDA (kąty wpisane oparte na tych samych łukach). To oznacza, że trójkąty ASD i CSB są podobne. Zatem

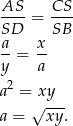
AS--= CS- SD SB a- x- y = a 2 a = xy a = √xy--.

Zatem 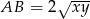√ --- AB = 2 xy .  
Odpowiedź: √ --- AB = 2 xy

Wersja PDF