/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Oblicz długość

Zadanie nr 5417431

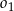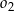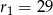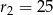Promienie okręgów o1 i o2 są równe odpowiednio r1 = 29 i r2 = 25 , a odległość między środkami tych okręgów jest równa 36. Oblicz długość odcinka łączącego punkty wspólne okręgów 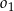o1 i o2 .

Wersja PDF

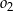Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

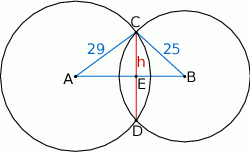
Zauważmy, że interesujący nas odcinek 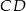CD jest dwa razy dłuższy od wysokości 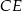CE trójkąta 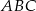ABC . Aby obliczyć tę wysokość obliczmy najpierw pole trójkąta 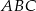ABC – znamy długości wszystkich jego boków, więc najprościej jest skorzystać ze wzoru Herona.

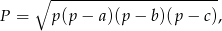
----------------------- ∘ P = p(p − a)(p − b )(p − c),

gdzie 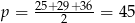p = 25+-229+36-= 45 jest połową obwodu trójkąta. Mamy więc

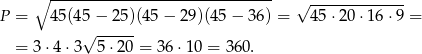
∘ ------------------------------- √ ------------- P = 45(45 − 2 5)(45− 29)(45 − 36) = 45⋅2 0⋅16 ⋅9 = √ ------ = 3⋅4 ⋅3 5 ⋅20 = 36⋅1 0 = 360.

Obliczamy teraz wysokość 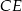CE .

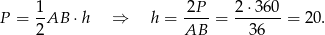
1- 2P-- 2⋅-360- P = 2AB ⋅h ⇒ h = AB = 36 = 2 0.

Odcinek 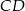CD jest dwa razy dłuższy, więc CD = 40 .  
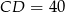Odpowiedź: 40

Wersja PDF