Zadanie nr 9849276
Dwa okręgi o środkach 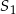 i
i 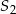 przecinają się w punktach
przecinają się w punktach 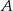 i
i 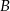 , przy czym punkty
, przy czym punkty 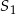 i
i 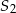 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 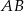 . Miary kątów
. Miary kątów 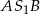 i
i 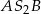 wynoszą odpowiednio
wynoszą odpowiednio 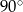 i
i 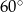 . Wyznacz długości promieni tych okręgów wiedząc, że
. Wyznacz długości promieni tych okręgów wiedząc, że 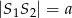 .
.
Rozwiązanie
Zaczynamy od rysunku.
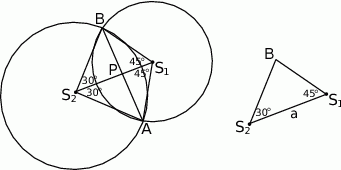
Sposób I
Oznaczmy 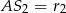 i
i 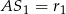 . Zauważmy, że trójkąt
. Zauważmy, że trójkąt 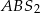 jest równoboczny (jest równoramienny i jeden z jego kątów ma miarę
jest równoboczny (jest równoramienny i jeden z jego kątów ma miarę 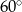 ). Zatem
). Zatem 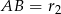 i ze wzoru na wysokość trójkąta równobocznego mamy
i ze wzoru na wysokość trójkąta równobocznego mamy
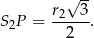
Ponadto trójkąt 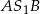 jest połówką kwadratu więc
jest połówką kwadratu więc
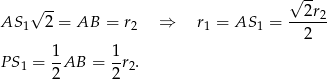
Korzystamy teraz z podanej długości odcinka 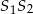 .
.
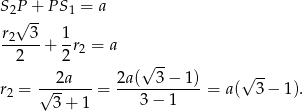
Zatem
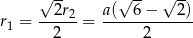
Sposób II
Jeżeli oznaczymy 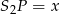 to mamy
to mamy
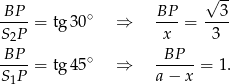
Z tych równości mamy
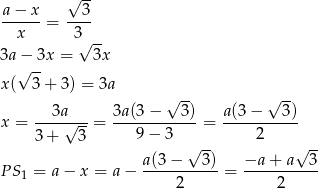
Promienie okręgów wyliczamy teraz z trójkątów 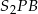 i
i 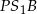 .
.
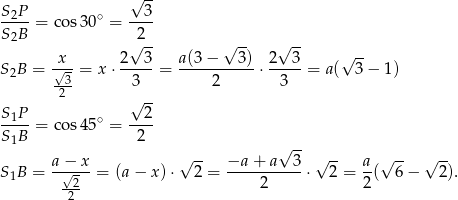
Sposób III
Tym razem popatrzmy na trójkąt 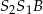 – znamy jego dwa kąty i bok, a chcemy wyliczyć długości pozostałych boków. Łatwo to zrobić z twierdzenia sinusów, o ile tylko wyliczymy sinus kąta
– znamy jego dwa kąty i bok, a chcemy wyliczyć długości pozostałych boków. Łatwo to zrobić z twierdzenia sinusów, o ile tylko wyliczymy sinus kąta 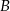 . Liczymy
. Liczymy
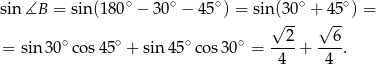
Korzystamy teraz z twierdzenia sinusów
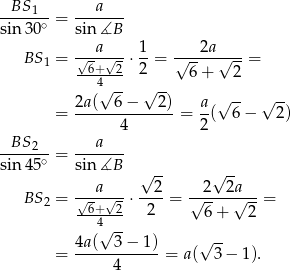
Odpowiedź: 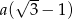 i
i