Zadanie nr 2272627
Zbadaj monotoniczność ciągu 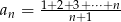 .
.
Rozwiązanie
W liczniku mamy sumę  kolejnych wyrazów ciągu arytmetycznego, więc
kolejnych wyrazów ciągu arytmetycznego, więc
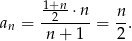
Ponieważ
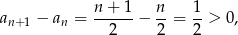
ciąg ten jest rosnący.
Odpowiedź: Ciąg rosnący.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Zbadaj monotoniczność ciągu 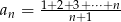 .
.
W liczniku mamy sumę  kolejnych wyrazów ciągu arytmetycznego, więc
kolejnych wyrazów ciągu arytmetycznego, więc
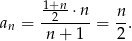
Ponieważ
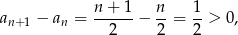
ciąg ten jest rosnący.
Odpowiedź: Ciąg rosnący.
