/Studia/Analiza/Ciągi

Zadanie nr 3074351

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz granicę 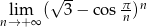√ -- π- n nl→im+∞ ( 3− co sn ) .

Rozwiązanie

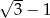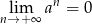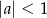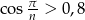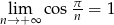Ciąg w nawiasie dąży do √ -- 3 − 1 , więc całość będzie dążyć do 0 (bo lim an = 0 n→+ ∞ dla |a | < 1 ). Aby to porządnie uzasadnić zauważmy, że definicji granicy ciągu, π- co sn > 0,8 dla dostatecznie dużych n (bo π- nl→im+∞ cos n = 1 ). Mamy wtedy

√ -- √ -- √ -- ( 3 − 1)n ≤ ( 3− co s π-)n < ( 3 − 0 ,8)n n

Skrajne ciągi dążą do 0, więc taka sama jest granica podanego ciągu.  
Odpowiedź: 0

Wersja PDF