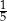/Studia/Analiza/Ciągi

Zadanie nr 5488731

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz granicę 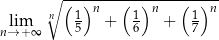∘ (--)n---(--)n---(--)n- lim n 1 + 1 + 1 n→ +∞ 5 6 7 .

Rozwiązanie

Korzystamy z twierdzenia o trzech ciągach. Patrzymy, który ze składników jest dominujący (najszybciej rośnie) pod pierwiastkiem, i w ten sposób odgadujemy jaka ma być granica.
Szacujemy

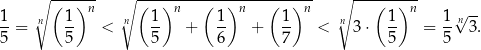
------- ------------------------- --------- ∘ ( )n ∘ ( )n ( )n ( )n ∘ ( )n √ -- 1-= n 1- < n 1- + 1- + 1- < n 3⋅ 1- = 1-n3 . 5 5 5 6 7 5 5

Skrajne ciągi dążą do 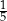1 5 , więc taka sama musi być granica danego ciągu.  
Odpowiedź: 1 5

Wersja PDF