/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Pole

Zadanie nr 3987691

W półkolu z końca średnicy poprowadzono cięciwę, która tworzy ze średnicą kąt o mierze 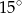15 ∘ . Oblicz w jakim stosunku zostało podzielone pole tego półkola.

Wersja PDF

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

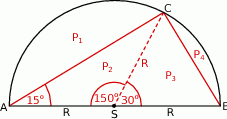
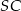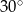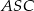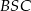Na rysunku narysowaliśmy promień SC , który przecina średnicę pod kątem 30∘ (twierdzenie o kącie wpisanym i środkowym). Znając kąty środkowe ASC i BSC łatwo obliczyć pola odpowiadających im wycinków koła.

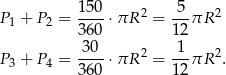
150 2 5 2 P1 + P2 = ----⋅πR = ---πR 360 12 P3 + P4 = -30-⋅πR 2 = -1-πR 2. 360 12

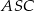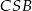Możemy też łatwo obliczyć pola trójkątów ASC i CSB – korzystamy ze wzoru z sinusem.

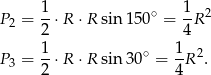
P 2 = 1-⋅R ⋅R sin 150∘ = 1R 2 2 4 1- ∘ 1- 2 P 3 = 2 ⋅R ⋅R sin 30 = 4 R .

Teraz łatwo obliczyć interesujący nas stosunek pól

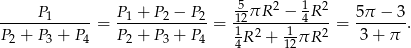
P1 P1 + P2 − P2 512πR 2 − 14R 2 5π − 3 P--+-P--+-P--= P--+-P--+-P--= 1--2---1----2-= 3-+-π--. 2 3 4 2 3 4 4R + 12πR

 
Odpowiedź: 5π3−+π3

Wersja PDF