Zadanie nr 3606391
Cięciwa 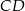 okręgu o środku
okręgu o środku 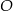 przecina średnicę
przecina średnicę 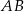 tego okręgu w punkcie
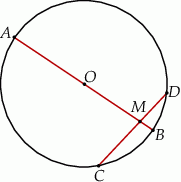
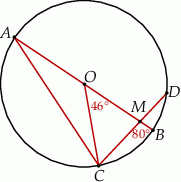
tego okręgu w punkcie 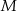 (rysunek). Kąt środkowy oparty na łuku
(rysunek). Kąt środkowy oparty na łuku 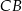 ma miarę
ma miarę 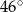 , a
, a 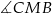 ma miarę
ma miarę 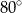 . Oblicz
. Oblicz 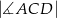 .
.
Rozwiązanie
Dorysujmy odcinki 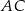 i
i 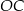 .
.
Ponieważ kąt wpisany jest zawsze połową kąta środkowego opartego na tym samym łuku, mamy
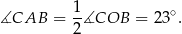
Ponadto
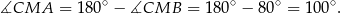
Patrzymy teraz na trójkąt 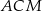 .
.
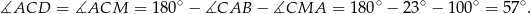
Odpowiedź: