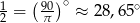/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Kąty

Zadanie nr 4402433

Wyznacz miarę łukową kąta środkowego w okręgu o promieniu 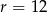r = 12 , opartego na łuku długości 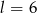l = 6 . Podaj miarę tego kąta w stopniach.

Wersja PDF

Rozwiązanie

Szkicujemy okrąg.

PIC

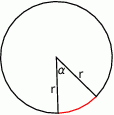
Cały okrąg ma długość 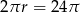2πr = 24π , zatem dany łuk stanowi

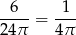
-6-- = -1- 24π 4π

długości całego okręgu. Czyli kąt środkowy oparty na tym łuku ma miarę w radianach:

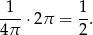
-1-⋅2π = 1. 4π 2

Po przeliczeniu na stopnie mamy

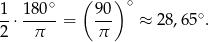
∘ ( ) ∘ 1-⋅ 180-= 90- ≈ 28 ,65∘. 2 π π

 
Odpowiedź: ( ) 1= 90 ∘ ≈ 2 8,65∘ 2 π

Wersja PDF