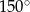Zadanie nr 7441744
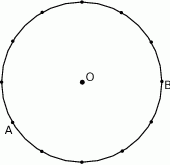
Punkty 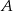 i
i 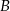 leżą na okręgu o środku
leżą na okręgu o środku 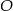 i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 7:5. Oblicz miarę kąta środkowego opartego na krótszym łuku.
i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 7:5. Oblicz miarę kąta środkowego opartego na krótszym łuku.
Rozwiązanie
Jeżeli podzielimy okrąg tak jak na obrazku na 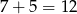 równych części,
równych części,
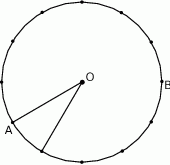
to kąt środkowy oparty na jednym małym łuku ma miarę
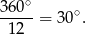
Kąt poparty na interesującym nas krótszym z łuków 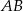 jest pięć razy większy, czyli ma miarę
jest pięć razy większy, czyli ma miarę
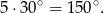
Odpowiedź: