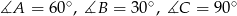/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Kąty

Zadanie nr 9508943

Z punktu 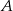A leżącego na okręgu poprowadź cięciwę 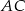AC o długości równej promieniowi okręgu oraz średnicę 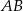AB . Wyznacz miary kątów wewnętrznych trójkąta ABC .

Wersja PDF

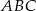Rozwiązanie

Rozpoczynamy oczywiście od rysunku.

PIC

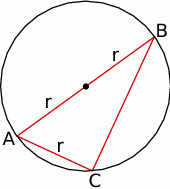
Zauważmy, że otrzymany trójkąt 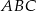ABC jest prostokątny (bo kąt 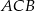ACB jest oparty na średnicy) oraz

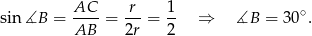
sin ∡B = AC--= r--= 1- ⇒ ∡B = 30 ∘. AB 2r 2

Stąd

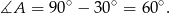
∡A = 90∘ − 30∘ = 60∘.

 
Odpowiedź: ∡A = 60∘, ∡B = 30∘, ∡C = 9 0∘

Wersja PDF