Zadanie nr 1707026
W ostrosłupie prawidłowym czworokątnym cosinus kąta między krawędziami bocznymi, które nie są sąsiednie jest równy 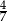 , a pole koła opisanego na podstawie ostrosłupa jest równe
, a pole koła opisanego na podstawie ostrosłupa jest równe 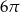 . Oblicz cosinus kąta
. Oblicz cosinus kąta  między sąsiednimi ścianami bocznymi ostrosłupa.
między sąsiednimi ścianami bocznymi ostrosłupa.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
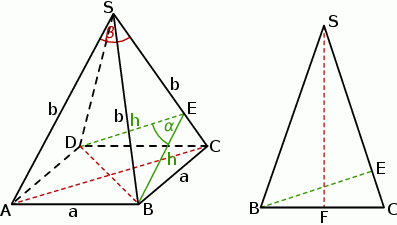
Promień okręgu opisanego na kwadracie w podstawie to po prostu połowa długości przekątnej, czyli 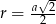 , gdzie przez
, gdzie przez  oznaczyliśmy długość krawędzi podstawy. Mamy zatem
oznaczyliśmy długość krawędzi podstawy. Mamy zatem
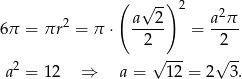
Spróbujemy teraz obliczyć długość 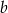 krawędzi bocznej ostrosłupa. Piszemy w tym celu twierdzenie cosinusów w trójkącie
krawędzi bocznej ostrosłupa. Piszemy w tym celu twierdzenie cosinusów w trójkącie 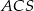 .
.
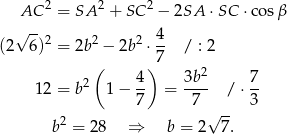
Jeżeli 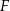 jest środkiem odcinka
jest środkiem odcinka 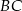 , to
, to
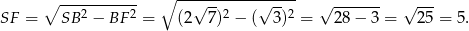
Aby zaznaczyć teraz kąt między sąsiednimi ścianami 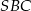 i
i 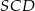 zaznaczamy rzut prostopadły
zaznaczamy rzut prostopadły 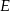 punktów
punktów 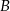 i
i 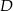 na krawędź
na krawędź 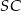 (płaszczyzna
(płaszczyzna 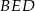 jest więc prostopadła do krawędzi
jest więc prostopadła do krawędzi 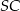 wspólnej płaszczyzn
wspólnej płaszczyzn 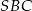 i
i 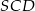 ). Długość odcinka
). Długość odcinka 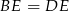 obliczamy porównując dwa wzory na pole trójkąta
obliczamy porównując dwa wzory na pole trójkąta 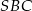 .
.
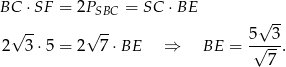
Teraz piszemy twierdzenie cosinusów w trójkącie 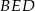 .
.
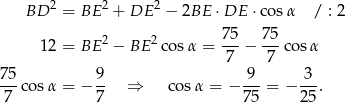
Odpowiedź: