/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Kąty

Zadanie nr 6615409

Wszystkie krawędzie ostrosłupa prawidłowego czworokątnego mają tę samą długość. Oblicz kąt nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku.

PIC

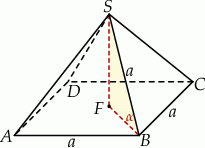
Sposób I

Patrząc na trójkąt prostokątny 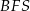BF S widać, że łatwo możemy wyliczyć cosinus szukanego kąta. Odcinek 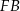F B to połowa przekątnej kwadratu w podstawie, zatem

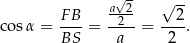
√- F B a-2- √ 2- cos α = --- = -2--= ---. BS a 2

Zatem 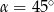∘ α = 4 5 .

Sposób II

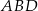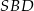Skoro wszystkie krawędzie są równe, to trójkąty ABD i SBD są przystające. Zatem szukany kąt jest równy kątowi 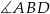∡ABD , który ma miarę ∘ 45 .  
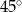Odpowiedź: 45∘

Wersja PDF