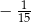/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Kąty

Zadanie nr 7153819

Dodaj do ulubionych
Dodaj do rozwiązanych

Krawędź boczna ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta między sąsiednimi ścianami bocznymi.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

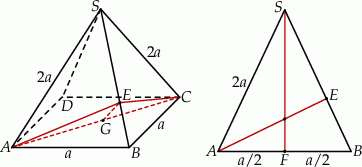
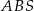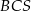Musimy na początek ustalić, jak zaznaczyć interesujący nas kąt między sąsiednimi ścianami bocznymi. Ponieważ trójkąty w ścianach bocznych są przystające, gdy opuścimy wysokości w trójkątach ABS i BCS na krawędź 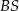BS to przetną one tę krawędź w tym samym punkcie 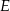E . I mamy to, o co nam chodziło: płaszczyzna 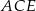ACE jest teraz prostopadła do krawędzi 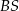BS , zatem interesujący nas kąt, to kąt przy wierzchołku 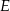E w trójkącie AEC .

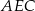Aby wyliczyć cosinus kąta 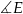∡E , możemy skorzystać z twierdzenia cosinusów w trójkącie 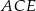ACE . Zanim to jednak zrobimy, wyliczmy boki tego trójkąta.

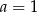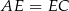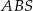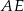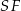Przyjmijmy, że krawędzie ostrosłupa mają długość a (równie dobrze możemy wziąć a = 1 , nie ma to żadnego znaczenia). Aby obliczyć długość odcinka AE = EC narysujmy z boku trójkąt ABS i jego wysokości AE i SF . Na mocy twierdzenia Pitagorasa

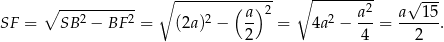
∘ ----------- ∘ --------(--)2- ∘ --------2 √ --- SF = SB2 − BF 2 = (2a)2 − a- = 4a 2 − a--= a---15. 2 4 2

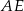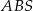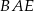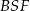Długość wysokości AE możemy obliczyć porównując dwa wzory na pole trójkąta ABS lub korzystając z podobieństwa trójkątów prostokątnych BAE i BSF . My wybierzemy tę drugą drogę. Na mocy wspomnianego podobieństwa mamy

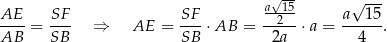
√-- √ --- AE-- SF- SF- a215- a--15- AB = SB ⇒ AE = SB ⋅AB = 2a ⋅a = 4 .

Dalszą część rozwiązania poprowadzimy na dwa sposoby.

Sposób I

Piszemy twierdzenie cosinusów w trójkącie 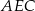AEC .

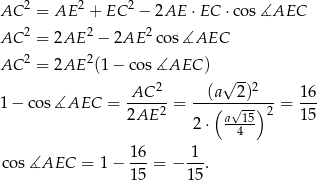
2 2 2 AC = AE + EC − 2AE ⋅ EC ⋅cos ∡AEC AC 2 = 2AE 2 − 2AE 2 cos∡AEC AC 2 = 2AE 2(1 − cos ∡AEC ) 2 √ --2 1 − cos ∡AEC = AC----= --((a--2))---= 1-6 2AE 2 a√15- 2 1 5 2⋅ 4 16 1 co s∡AEC = 1− ---= − --. 15 15

Nie należy się bać ujemnego cosinusa – po prostu kąt 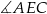∡AEC jest rozwarty.

Sposób II

Tym razem obejdziemy się bez twierdzenia cosinusów. Niech 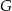G będzie środkiem odcinka 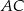AC . Ponieważ trójkąt 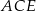ACE jest równoramienny, mamy 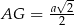a√2 AG = -2-- oraz

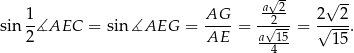
√- √ -- 1 AG a22- 2 2 sin 2-∡AEC = sin ∡AEG = AE--= a√-15= √----. --4-- 15

Teraz korzystamy ze wzoru na 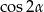cos2 α .

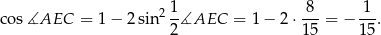
cos∡AEC = 1 − 2 sin 2 1-∡AEC = 1 − 2 ⋅-8-= − -1-. 2 15 15

 
Odpowiedź: − 115

Wersja PDF