/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Kąty

Zadanie nr 9218296

Dodaj do ulubionych
Dodaj do rozwiązanych

Objętość ostrosłupa prawidłowego czworokątnego 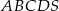ABCDS o podstawie 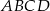ABCD jest równa 224, a promień okręgu opisanego na podstawie 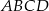ABCD jest równy 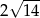√ --- 2 14 . Oblicz cosinus kąta między wysokością tego ostrosłupa i jego ścianą boczną.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

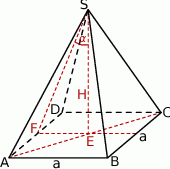
Promień okręgu opisanego na kwadracie w podstawie to po prostu połowa długości przekątnej, czyli

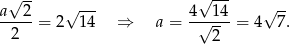
√ -- √ --- a--2- √ --- 4--14- √ -- 2 = 2 14 ⇒ a = √ -- = 4 7. 2

Z danej objętości obliczamy wysokość ostrosłupa.

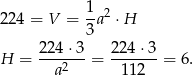
1-2 224 = V = 3a ⋅ H H = 224-⋅3-= 224-⋅3-= 6. a2 11 2

Z trójkąta prostokątnego 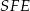SF E obliczamy wysokość 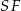SF ściany bocznej.

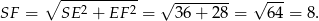
∘ ---2------2 √ -------- √ --- SF = SE + EF = 36 + 28 = 64 = 8.

Pozostało obliczyć interesujący nas cosinus kąta między wysokością ostrosłupa, a ścianą boczną.

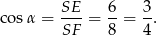
cos α = SE-= 6-= 3. SF 8 4

 
Odpowiedź: 34

Wersja PDF