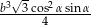/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy trójkątny/Objętość

Zadanie nr 6802962

Dodaj do ulubionych
Dodaj do rozwiązanych

Krawędź boczna ostrosłupa prawidłowego trójkątnego ma długość 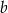b i tworzy z płaszczyzną podstawy kąt o mierze α . Jaką objętość ma ten ostrosłup?

Rozwiązanie

Zaczynamy od schematycznego rysunku.

PIC

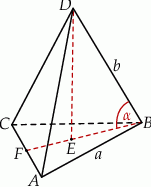
Z trójkąta prostokątnego 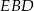EBD obliczamy wysokość ostrosłupa.

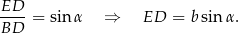
ED--= sin α ⇒ ED = bsin α. BD

Z tego samego trójkąta obliczamy długość odcinka 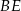BE .

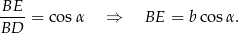
BE ----= co sα ⇒ BE = bcos α. BD

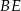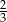Z drugiej strony, BE to 2 3 wysokości trójkąta 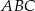ABC , czyli

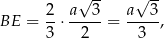
-- -- 2 a√ 3 a√ 3 BE = --⋅-----= -----, 3 2 3

gdzie przez a oznaczyliśmy krawędź trójkąta w podstawie. Mamy więc

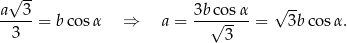
√ -- √ -- a--3-= bco sα ⇒ a = 3b√cosα-= 3b cosα. 3 3

Liczymy teraz objętość (korzystamy ze wzoru na pole trójkąta równobocznego).

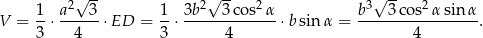
2√ -- 2√ -- 2 3√ -- 2 V = 1-⋅ a--3-⋅ED = 1-⋅ 3b--3-cos-α-⋅ bsinα = b---3-cos-α-sinα-. 3 4 3 4 4

 
Odpowiedź: √- b3-3-cos2αsinα 4

Wersja PDF