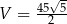/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy trójkątny/Objętość

Zadanie nr 8803304

Dodaj do ulubionych
Dodaj do rozwiązanych

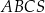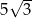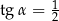Długość krawędzi bocznej ostrosłupa prawidłowego trójkątnego ABCS jest równa √ -- 5 3 (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt α taki, że tg α = 1 2 . Oblicz objętość tego ostrosłupa.

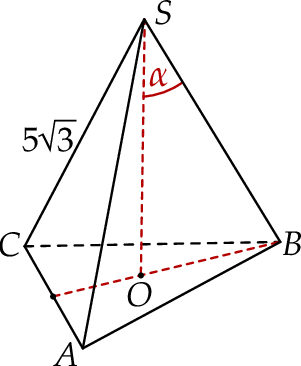
ZINFO-FIGURE

Rozwiązanie

Oznaczmy przez 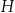H wysokość ostrosłupa. Wtedy z podanego tangensa kąta α mamy

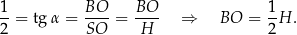
1-= tg α = BO--= BO-- ⇒ BO = 1H . 2 SO H 2

Piszemy teraz twierdzenie Pitagorasa w trójkącie prostokątnym 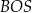BOS .

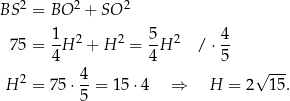
BS 2 = BO 2 + SO 2 7 5 = 1-H2 + H 2 = 5H 2 / ⋅ 4 4 4 5 2 4- √ --- H = 75 ⋅5 = 15⋅4 ⇒ H = 2 15.

Jeżeli ponadto oznaczymy 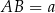AB = a , to

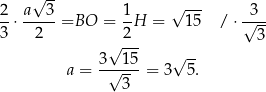
√ -- 2- a--3- 1- √ --- -3-- 3 ⋅ 2 =BO = 2H = 15 / ⋅√ 3 √ --- a = 3-√-15 = 3√ 5-. 3

Objętość ostrosłupa jest więc równa

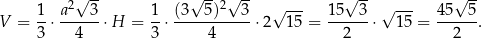
√ -- √ -- √ -- √ -- √ -- 1 a2 3 1 (3 5)2 3 √ --- 15 3 √ --- 45 5 V = --⋅------⋅H = -⋅ -----------⋅2 15 = ------⋅ 15 = ------. 3 4 3 4 2 2

 
Odpowiedź: √ - V = 45--5 2

Wersja PDF