Zadanie nr 9444392
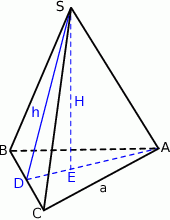
W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej prostopadła do krawędzi podstawy ostrosłupa jest równa 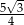 , a pole powierzchni bocznej tego ostrosłupa jest równe
, a pole powierzchni bocznej tego ostrosłupa jest równe 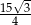 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Rozwiązanie
Oznaczmy przez  krawędź podstawy ostrosłupa, a przez
krawędź podstawy ostrosłupa, a przez 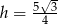 wysokość ściany bocznej.
wysokość ściany bocznej.
Z podanego pola powierzchni bocznej mamy
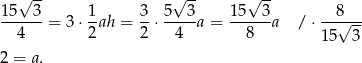
Musimy jeszcze obliczyć wysokość 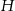 ostrosłupa. Zrobimy to z trójkąta prostokątnego
ostrosłupa. Zrobimy to z trójkąta prostokątnego 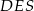 , ale najpierw zauważmy, że
, ale najpierw zauważmy, że 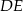 to
to 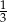 wysokości trójkąta równobocznego w podstawie ostrosłupa, więc
wysokości trójkąta równobocznego w podstawie ostrosłupa, więc
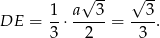
Mamy zatem
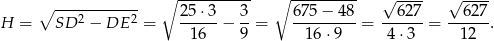
Objętość ostrosłupa jest więc równa
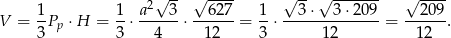
Odpowiedź: