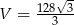/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy trójkątny/Objętość

Zadanie nr 9655898

Krawędź boczna ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny podstawy pod kątem 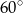6 0∘ . Odległość spodka wysokości ostrosłupa od krawędzi bocznej jest równa 4. Oblicz objętość tego ostrosłupa.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku

PIC

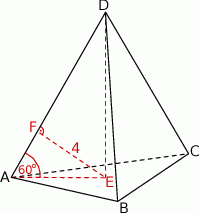
Trójkąt 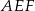AEF jest prostokątny, więc możemy zastosować funkcję trygonometryczną do obliczenia długości odcinka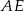 AE

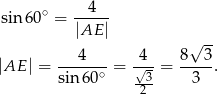
sin 60∘ = --4-- |AE | √ -- |AE | = ---4--- = -4√- = 8--3. sin6 0∘ -3- 3 2

Punkt 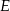E jest środkiem ciężkości trójkąta równobocznego 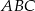ABC , więc jeżeli oznaczymy przez 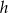h wysokość podstawy, to

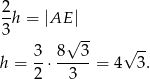
2 -h = |AE | 3 √ -- 3- 8--3- √ -- h = 2 ⋅ 3 = 4 3 .

Teraz możemy łatwo obliczyć długość boku podstawy

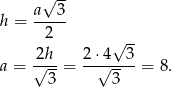
√ -- a--3- h = 2 √ -- a = 2√h--= 2⋅√4--3-= 8. 3 3

Korzystamy z funkcji trygonometrycznych żeby obliczyć wysokość ostrosłupa

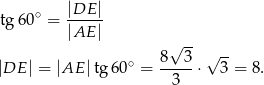
tg6 0∘ = |DE-| |AE | 8√ 3- √ -- |DE | = |AE |tg60 ∘ = -----⋅ 3 = 8 . 3

Teraz już łatwo obliczyć objętość

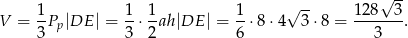
√ -- √ -- V = 1-Pp|DE | = 1-⋅ 1-ah|DE | = 1-⋅8 ⋅4 3 ⋅8 = 128--3. 3 3 2 6 3

 
Odpowiedź: √- V = 1283-3

Wersja PDF