/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy trójkątny/Pole powierzchni

Zadanie nr 7328675

Objętość ostrosłupa prawidłowego trójkątnego 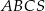ABCS jest równa 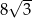√ -- 8 3 . Długość krawędzi 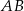AB podstawy ostrosłupa jest równa 4 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.

PIC

Wersja PDF

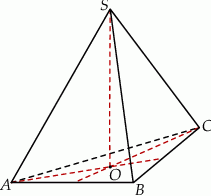
Rozwiązanie

Dorysujmy wysokość ściany bocznej ostrosłupa.

PIC

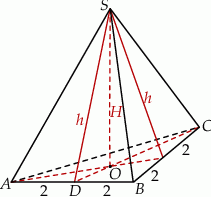
Korzystając z podanej objętości obliczamy wysokość 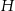H ostrosłupa.

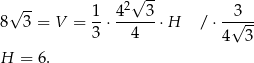
2√ -- 8 √ 3 = V = 1-⋅ 4--3-⋅H / ⋅-√3-- 3 4 4 3 H = 6.

Teraz z trójkąta prostokątnego 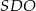SDO obliczymy wysokość 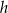h ściany bocznej. Zanim jednak to zrobimy, obliczmy długość odcinka 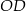OD – jest to 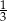13 wysokości trójkąta równobocznego w podstawie.

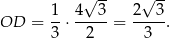
√ -- √ -- 1- 4--3- 2--3- OD = 3 ⋅ 2 = 3 .

Stosujemy teraz twierdzenie Pitagorasa w trójkącie 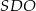SDO .

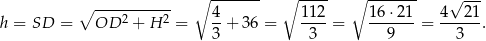
∘ ------- ∘ ---- ∘ ------- √ --- ∘ ----------- 4 112 1 6⋅21 4 21 h = SD = OD 2 + H 2 = --+ 36 = ----= -------= ------. 3 3 9 3

Pozostało obliczyć pole powierzchni całkowitej.

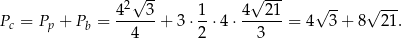
2√ -- √ --- P = P + P = 4---3-+ 3⋅ 1⋅ 4⋅ 4--21-= 4 √ 3+ 8√ 21. c p b 4 2 3

 
Odpowiedź: √ -- √ --- 4 3 + 8 2 1

Wersja PDF