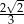Zadanie nr 5062238
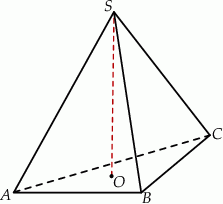
W ostrosłupie prawidłowym trójkątnym  pole powierzchni bocznej jest trzy razy większe od pola podstawy. Oblicz sinus kąta nachylenia ściany bocznej tego ostrosłupa do płaszczyzny jego podstawy.
pole powierzchni bocznej jest trzy razy większe od pola podstawy. Oblicz sinus kąta nachylenia ściany bocznej tego ostrosłupa do płaszczyzny jego podstawy.
Rozwiązanie
Oznaczmy przez  długość krawędzi podstawy, a przez
długość krawędzi podstawy, a przez 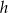 i
i 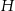 odpowiednio długości wysokości ściany bocznej oraz wysokości ostrosłupa.
odpowiednio długości wysokości ściany bocznej oraz wysokości ostrosłupa.
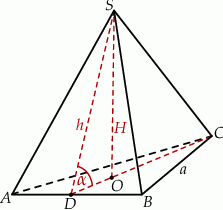
Sposób I
Z podanego stosunku pola bocznego do pola podstawy mamy
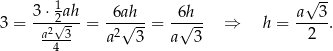
Ponieważ środek  trójkąta równobocznego
trójkąta równobocznego 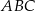 dzieli jego wysokość
dzieli jego wysokość 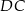 w stosunku 2:1, mamy
w stosunku 2:1, mamy
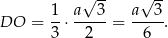
Z trójkąta prostokątnego 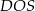 obliczamy teraz wysokość ostrosłupa.
obliczamy teraz wysokość ostrosłupa.
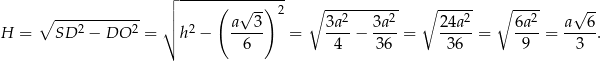
Stąd
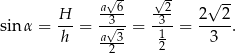
Sposób II
Zauważmy, że z treści zadania wynika, że ściany boczne są przystającymi trójkątami równoramiennymi o polu takim samym jak pole podstawy ostrosłupa. To oznacza, że ściany boczne są trójkątami równobocznymi i mamy do czynienia z czworościanem foremnym. W szczególności
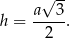
Resztę rachunków przeprowadzamy tak samo jak w pierwszym sposobie.
Odpowiedź: