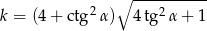Zadanie nr 1656378
Odległość środka wysokości ostrosłupa prawidłowego trójkątnego od ściany bocznej jest równa  . Krawędź boczna tworzy z płaszczyzną podstawy kąt
. Krawędź boczna tworzy z płaszczyzną podstawy kąt  . Oblicz objętość i pole powierzchni całkowitej ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej ostrosłupa.
Rozwiązanie
Zaczynamy od rysunku
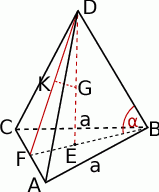
Plan jest następujący: ponieważ 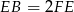 ze znanego
ze znanego 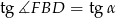 łatwo obliczyć
łatwo obliczyć 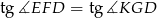 . To pozwoli nam wyliczyć
. To pozwoli nam wyliczyć 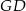 w zależności od
w zależności od 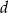 . Mając wysokość ostrosłupa wyliczymy długość
. Mając wysokość ostrosłupa wyliczymy długość  krawędzi podstawy i wysokość ściany bocznej.
krawędzi podstawy i wysokość ściany bocznej.
Zatem do dzieła. Z podobieństwa trójkątów 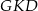 i
i 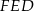 mamy
mamy
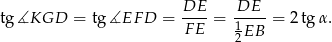
Jeżeli oznaczymy 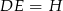 , to z trójkąta
, to z trójkąta 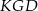 mamy
mamy
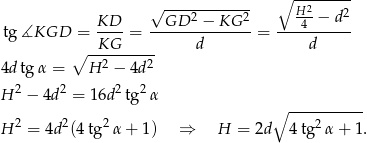
Teraz już łatwo. Ponieważ środek trójkąta równobocznego dzieli jego wysokość w stosunku 2:1, więc ze wzoru na wysokość w trójkącie równobocznym.
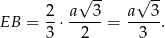
Patrzymy teraz na trójkąt 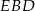 .
.
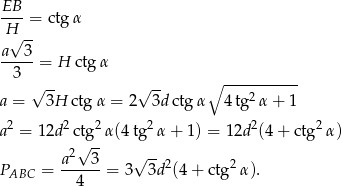
Teraz już możemy policzyć objętość:
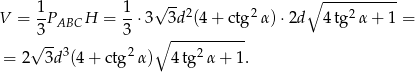
Do wyliczenia pola powierzchni potrzebujemy jeszcze znać wysokość ściany bocznej. Spróbujemy wyznaczyć tę wysokość w zależności  – licząc pole i tak będziemy mnożyć przez
– licząc pole i tak będziemy mnożyć przez  , a
, a 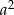 mamy już ładnie wyliczone. Jak już wcześniej wyliczyliśmy
mamy już ładnie wyliczone. Jak już wcześniej wyliczyliśmy
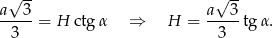
Zatem
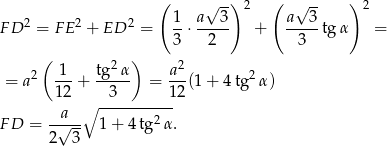
Zatem pole ściany bocznej jest równe
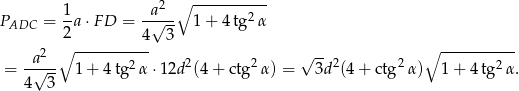
Zatem pole powierzchni jest równe
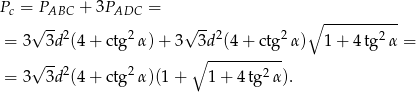
Odpowiedź: 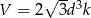 ,
, 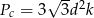 , gdzie
, gdzie