Zadanie nr 3041458
W sferę o promieniu 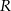 wpisano ostrosłup prawidłowy trójkątny w ten sposób, że wszystkie wierzchołki ostrosłupa leżą na powierzchni sfery. Wiedząc, że krawędź boczna ostrosłupa ma długość 13, a krawędź podstawy długość
wpisano ostrosłup prawidłowy trójkątny w ten sposób, że wszystkie wierzchołki ostrosłupa leżą na powierzchni sfery. Wiedząc, że krawędź boczna ostrosłupa ma długość 13, a krawędź podstawy długość 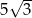 , oblicz
, oblicz 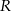 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
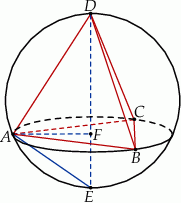
Zauważmy, że prosta 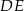 zawierająca wysokość ostrosłupa zawiera też średnicę sfery, czyli trójkąt
zawierająca wysokość ostrosłupa zawiera też średnicę sfery, czyli trójkąt 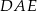 jest prostokątny (kąt
jest prostokątny (kąt 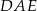 jest oparty na średnicy). Ponadto
jest oparty na średnicy). Ponadto 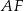 jest wysokością tego trójkąta. Obliczmy długość tego odcinka – ma on długość
jest wysokością tego trójkąta. Obliczmy długość tego odcinka – ma on długość  wysokości trójkąta równobocznego
wysokości trójkąta równobocznego 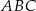 , czyli
, czyli
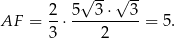
Stąd (twierdzenie Pitagorasa w trójkącie 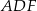 )
)
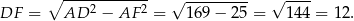
Teraz wystarczy zauważyć, że trójkąty prostokątne 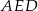 i
i 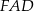 są podobne (mają wspólny kąt
są podobne (mają wspólny kąt 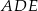 ). Mamy więc
). Mamy więc
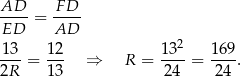
Odpowiedź: