Zadanie nr 7274654
Podstawą ostrosłupa 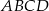 jest trójkąt równoboczny
jest trójkąt równoboczny 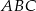 o boku długości
o boku długości 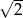 . Wszystkie ściany boczne są równoramiennymi trójkątami prostokątnymi. Punkt
. Wszystkie ściany boczne są równoramiennymi trójkątami prostokątnymi. Punkt 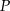 został wybrany wewnątrz ostrosłupa w ten sposób, że wysokości ostrosłupów
został wybrany wewnątrz ostrosłupa w ten sposób, że wysokości ostrosłupów 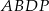 ,
, 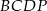 ,
, 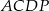 ,
, 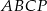 opuszczone z wierzchołka
opuszczone z wierzchołka 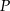 mają tę samą długość
mają tę samą długość 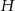 . Sporządź rysunek ostrosłupa i oblicz
. Sporządź rysunek ostrosłupa i oblicz 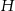 .
.
Rozwiązanie
Jak to w zadaniach geometrycznych, najważniejszy jest porządny (duży i wyraźny) rysunek.
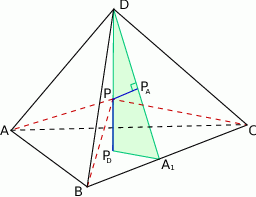
Sposób I
Przyjmijmy oznaczenia jak na rysunku, tzn. 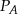 i
i 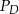 rzuty
rzuty 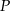 na ściany przeciwległe do wierzchołków
na ściany przeciwległe do wierzchołków 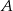 i
i 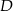 odpowiednio,
odpowiednio, 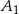 – rzut
– rzut 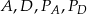 na krawędź
na krawędź 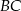 . Wartość
. Wartość 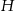 obliczymy z zielonego trójkąta, więc powyliczajmy najpierw niektóre jego odcinki.
obliczymy z zielonego trójkąta, więc powyliczajmy najpierw niektóre jego odcinki. 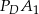 jest promieniem okręgu wpisanego w trójkąt równoboczny
jest promieniem okręgu wpisanego w trójkąt równoboczny 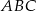 (albo, jak ktoś woli jest to
(albo, jak ktoś woli jest to 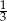 długości wysokości tego trójkąta), więc ze znanych wzorów
długości wysokości tego trójkąta), więc ze znanych wzorów
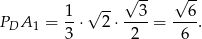
Ponieważ trójkąt 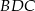 jest równoramienny i prostokątny, więc
jest równoramienny i prostokątny, więc 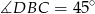 . Zatem trójkąt
. Zatem trójkąt 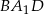 jest równoramienny (bo jest prostokątny i jeden z kątów ma miarę
jest równoramienny (bo jest prostokątny i jeden z kątów ma miarę 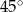 ). Stąd
). Stąd
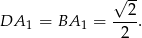
Możemy zatem wyliczyć 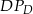
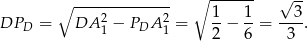
No i teraz gwóźdź programu, czyli układamy proporcję dla trójkątów podobnych 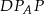 i
i 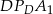 :
:
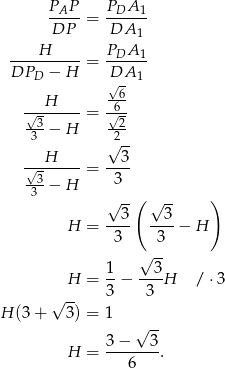
Sposób II
Tym razem 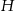 wyliczymy porównując objętość całego ostrosłupa z sumą objętości czterech ostrosłupów, na które został podzielony.
wyliczymy porównując objętość całego ostrosłupa z sumą objętości czterech ostrosłupów, na które został podzielony.
Ponieważ trójkąty w ścianach bocznych są prostokątne i równoramienne, więc
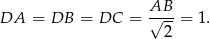
Pola tych trójkątów są więc równe
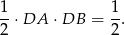
Pole podstawy jest równe
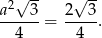
Obliczmy jeszcze wysokość dużego ostrosłupa. Liczymy z twierdzenia Pitagorasa.
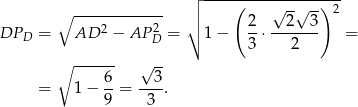
Teraz zgodnie z zapowiedzią porównujemy objętość ostrosłupa z sumą objętości ostrosłupów 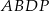 ,
, 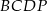 ,
, 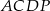 ,
, 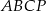 .
.
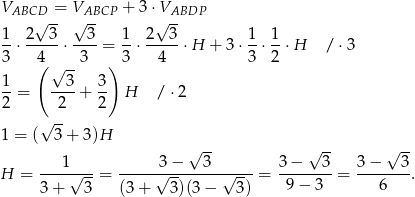
Odpowiedź: