Zadanie nr 7380409
Wysokość ostrosłupa prawidłowego trójkątnego jest dwa razy krótsza od promienia okręgu opisanego na podstawie tego ostrosłupa, a jego objętość jest równa 9. Oblicz pole powierzchni bocznej ostrosłupa oraz tangens kąta, jaki tworzy krawędź boczna z krawędzią podstawy ostrosłupa.
Rozwiązanie
Oznaczmy przez  długość krawędzi podstawy ostrosłupa.
długość krawędzi podstawy ostrosłupa.
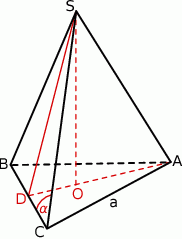
Pole podstawy jest równe 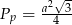 , a wysokość trójkąta w podstawie jest równa
, a wysokość trójkąta w podstawie jest równa
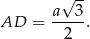
Wiemy ponadto, że
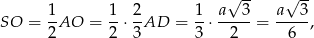
więc z podanej objętości ostrosłupa możemy obliczyć  .
.
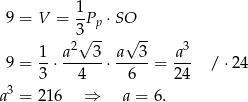
Mamy zatem
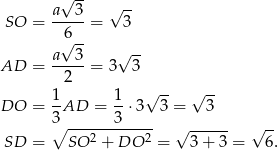
Pole powierzchni bocznej jest więc równe
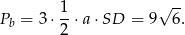
Obliczamy jeszcze tangens kąta 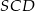 .
.
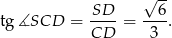
Odpowiedź: 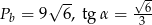 .
.

