/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy trójkątny/Różne

Zadanie nr 8417219

W ostrosłupie prawidłowym trójkątnym krawędzie boczne są dwa razy dłuższe od krawędzi podstawy.

  1. Wyznacz sinus kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy.
  2. Wyznacz długość krawędzi podstawy, tak aby objętość ostrosłupa wynosiła √ --- 23 11 .
Wersja PDF

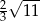Rozwiązanie

Zaczynamy od rysunku

PIC

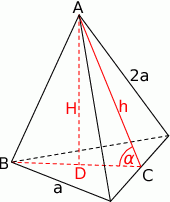
  • Obliczamy wysokość trójkąta w podstawie
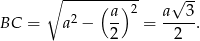
    ∘ ----------- √ -- 2 ( a) 2 a--3- BC = a − 2 = 2 .

    Odcinek 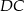DC stanowi 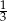1 3 wysokości, czyli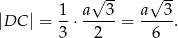

    √ -- √ -- 1- a--3- a--3- |DC | = 3 ⋅ 2 = 6 .

    Obliczamy wysokość ściany bocznej

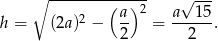
    ∘ --------(--)-- √ --- h = (2a )2 − a- 2 = a--15-. 2 2

    Z twierdzenia Pitagorasa obliczamy wysokość ostrosłupa

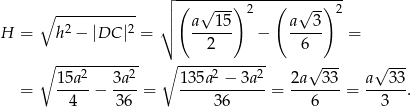
    ┌│ (------)-----(------)-- ∘ ----------- │ a√ 15 2 a√ 3 2 H = h2 − |DC |2 = ∘ ------ − ----- = 2 6 ∘ ----2-----2- ∘ -----2-----2 √ --- √ --- = 15a--− 3a--= 135a--−-3a--= 2a--3-3 = a---33. 4 36 36 6 3

    Teraz już łatwo obliczyć sinus

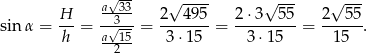
    -- a√-33 √ ---- √ --- √ --- sin α = H- = -√3-- = 2--4-95 = 2⋅3--5-5-= 2---55. h a--15 3 ⋅15 3 ⋅15 15 2

     
    Odpowiedź: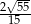 √-- 21555-

  • Objętość ostrosłup jest równa
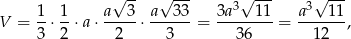
    1 1 a√ 3- a√ 33- 3a 3√ 1-1 a 3√ 11- V = --⋅--⋅a⋅ -----⋅------= -------- = -------, 3 2 2 3 36 1 2

    co prowadzi do równania

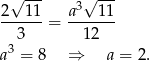
    --- --- 2√ 11 a3√ 11 ------= ------- 3 12 a3 = 8 ⇒ a = 2.

     
    Odpowiedź: 2

Wersja PDF