/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy trójkątny/Różne

Zadanie nr 9005121

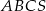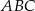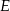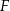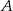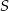Podstawą ostrosłupa prawidłowego trójkątnego ABCS jest trójkąt ABC . Punkty E i F są rzutami punktów A i S na przeciwległe ściany. Oblicz w jakim stosunku odcinek 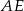AE dzieli odcinek 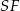SF , jeżeli ściana boczna ostrosłupa jest nachylona do podstawy pod kątem, którego sinus jest równy a .

Wersja PDF

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

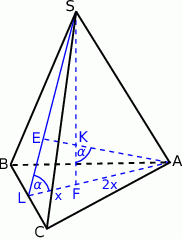
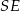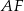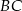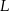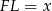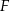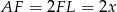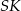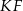Ponieważ ostrosłup jest prawidłowy, odcinki SE i AF przecinają się w środku krawędzi BC – oznaczmy ten punkt przez L . Niech FL = x . Ponieważ punkt F jest środkiem trójkąta równobocznego w podstawie, AF = 2FL = 2x . Spróbujemy obliczyć długości odcinków SK i KF w zależności od α i x .

Zauważmy, że trójkąt 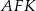AF K jest prostokątny i ma kąt wspólny z trójkątem 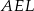AEL , jest więc do niego podobny. W szczególności 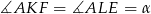∡AKF = ∡ALE = α . Zatem

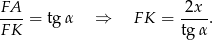
FA-- -2x- FK = tgα ⇒ FK = tg α.

Teraz patrzymy na trójkąt prostokątny 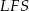LF S .

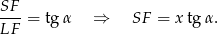
SF LF- = tg α ⇒ SF = x tg α.

Stąd

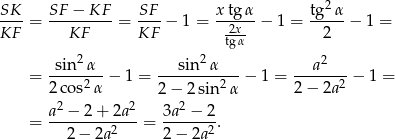
SK-- SF-−-KF-- SF-- xtg-α- tg2-α KF = KF = KF − 1 = 2x- − 1 = 2 − 1 = tg α sin 2α sin2 α a2 = ----2---− 1 = --------2--− 1 = ------2-− 1 = 2co s α 2− 2sin α 2 − 2a a2 − 2+ 2a2 3a 2 − 2 = --2-−-2a2--- = 2-−-2a-2.

 
Odpowiedź: 3a2−2 2− 2a2

Wersja PDF