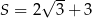/Szkoła średnia/Ciągi/Szereg geometryczny

Zadanie nr 1859383

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozważamy nieskończone ciągi geometryczne o ilorazie 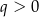q > 0 , w których kwadrat drugiego wyrazu jest dodatni i równy sumie wyrazów: drugiego, trzeciego i czwartego. Wyznacz pierwszy wyraz i iloraz tego spośród rozpatrywanych ciągów, którego suma wszystkich wyrazów jest najmniejsza. Oblicz tę sumę.

Rozwiązanie

Zapiszmy warunek opisany w treści zadania.

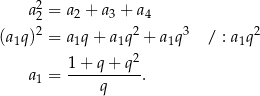
2 a2 = a2 + a3 + a4 (a1q)2 = a1q + a1q2 + a1q3 / : a1q2 2 a = 1-+-q-+-q- . 1 q

Suma wszystkich wyrazów ciągu (an) jest więc równa

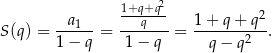
1+q+q2- 2 S (q) = --a1--= ---q---= 1-+-q+--q-. 1 − q 1− q q − q2

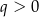Dziedziną tej funkcji jest przedział (0,1) (bo z założenia q > 0 ). Liczymy pochodną tej funkcji

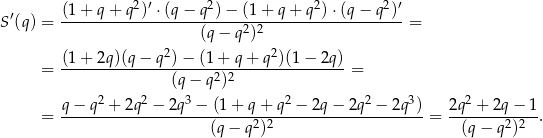
′ (1-+-q-+-q2)′ ⋅(q-−-q2)-−-(1-+-q-+-q2)⋅-(q−-q2)′ S (q) = (q − q2)2 = (1-+-2q)(q-−-q2)-−-(1-+-q-+-q2)(1-−-2q) = (q − q2)2 = 2 2 3 2 2 3 2 = q-−-q--+-2q--−-2q--−-(1-+-q-+-q-−--2q−--2q-−--2q-) = 2q-+--2q−--1. (q− q2)2 (q − q2)2

Rozkładamy teraz trójmian w liczniku.

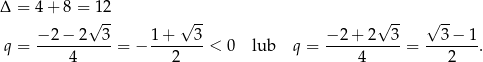
Δ = 4 + 8 = √12- √ -- √ -- √ -- − 2− 2 3 1 + 3 − 2 + 2 3 3 − 1 q = -----------= − --------< 0 lub q = ----------- = --------. 4 2 4 2

Zatem

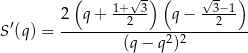
( √-) ( √- ) 2 q + 1+2-3 q − -32−1- S′(q) = ---------------2-2-------- (q− q )

i pochodna jest ujemna w przedziale 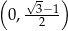( √ 3−1) 0,--2-- oraz dodatnia w przedziale 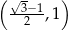(√-3−1 ) 2 ,1 . To oznacza, że funkcja 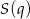S(q) jest malejąca w przedziale 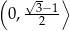( √-3−-1⟩ 0, 2 i rosnąca w 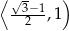⟨ ) √-3−1 2 ,1 . Najmniejszą wartość sumy otrzymamy więc dla 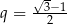√- q = -3−-1 2 . Pierwszy wyraz ciągu jest wtedy równy

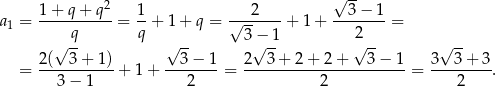
√ -- 1 + q + q2 1 2 3− 1 a1 = ---------- = --+ 1 + q = √-------+ 1+ --------= √ -q q √ -- 3 −√ 1- √2-- √ -- 2( 3 + 1) 3− 1 2 3+ 2 + 2 + 3 − 1 3 3 + 3 = -----------+ 1 + --------= -----------------------= ---------. 3− 1 2 2 2

Suma ciągu jest równa

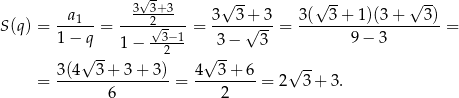
3√-3+3- √ -- √ -- √ -- S (q) = --a1--= ----2√-----= 3--3+√--3-= 3-(--3+--1)(3+----3) = 1 − q 1− --3−-1 3 − 3 9− 3 √ -- 2 √ -- 3(4--3-+-3-+-3-) 4--3-+-6- √ -- = 6 = 2 = 2 3 + 3.

 
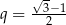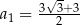Odpowiedź: √- q = -3−2-1 , √ - a1 = 3--32+3 , √ -- S = 2 3 + 3

Wersja PDF