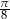Zadanie nr 1942915
W trójkąt równoboczny  o boku długości 1 wpisano koło. Prowadzimy proste równoległe do boków trójkąta
o boku długości 1 wpisano koło. Prowadzimy proste równoległe do boków trójkąta  i styczne do koła wpisanego. Proste te odcinają od trójkąta
i styczne do koła wpisanego. Proste te odcinają od trójkąta  trzy trójkąty równoboczne. W każdy z nich wpisujemy koło i postępujemy analogicznie jak z kołem wpisanym w trójkąt
trzy trójkąty równoboczne. W każdy z nich wpisujemy koło i postępujemy analogicznie jak z kołem wpisanym w trójkąt  . Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę pól wszystkich otrzymanych w ten sposób kół.
. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę pól wszystkich otrzymanych w ten sposób kół.
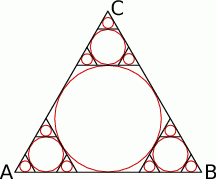
Rozwiązanie
Zauważmy najpierw, że pierwsze z kół ma promień
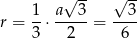
i pole
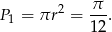
Spróbujmy teraz zrozumieć jak promień kolejnego koła powstaje z promienia  poprzedniego koła.
poprzedniego koła.
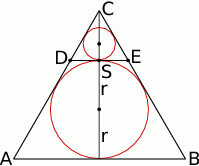
Zauważmy, że ponieważ średnica okręgu wpisanego w trójkąt równoboczny stanowi  wysokości trójkąta
wysokości trójkąta 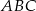 , trójkąt
, trójkąt 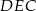 jest trzy razy mniejszy od trójkąta
jest trzy razy mniejszy od trójkąta 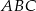 . W takim razie pole koła wpisanego w ten trójkąt jest dziewięć razy mniejsze od pola koła wpisanego w trójkąt
. W takim razie pole koła wpisanego w ten trójkąt jest dziewięć razy mniejsze od pola koła wpisanego w trójkąt 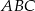 . Są jednak trzy koła tej wielkości, więc suma pól
. Są jednak trzy koła tej wielkości, więc suma pól 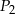 kół otrzymanych w kolejnym kroku jest równa
kół otrzymanych w kolejnym kroku jest równa
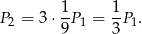
I tak dalej, w każdym kolejnym kroku suma pól będzie zmniejszać się o 3. W takim razie suma wszystkich pól jest równa
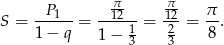
Odpowiedź: