Zadanie nr 2013255
Dane jest koło 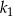 o promieniu
o promieniu  . W tym kole narysowano koło
. W tym kole narysowano koło 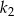 styczne wewnętrznie, którego pole jest równe połowie pola koła
styczne wewnętrznie, którego pole jest równe połowie pola koła 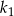 . W kole
. W kole 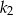 narysowano koło
narysowano koło 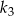 styczne wewnętrznie, którego pole jest równe połowie pola koła
styczne wewnętrznie, którego pole jest równe połowie pola koła 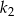 . Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę obwodów wszystkich narysowanych kół.
. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę obwodów wszystkich narysowanych kół.
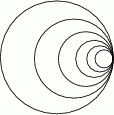
Rozwiązanie
Wiemy, że każde kolejne koło ma pole dwa razy mniejsze od poprzedniego koła. To oznacza, że promień każdego koła stanowi 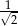 promienia poprzedniego koła (korzystamy tu ze wzoru na pole koła, lub z tego, że pole zmienia się jak kwadrat skali podobieństwa). Obwody kolejnych kół tworzą więc ciąg geometryczny
promienia poprzedniego koła (korzystamy tu ze wzoru na pole koła, lub z tego, że pole zmienia się jak kwadrat skali podobieństwa). Obwody kolejnych kół tworzą więc ciąg geometryczny 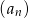 o pierwszym wyrazie
o pierwszym wyrazie 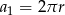 i ilorazie
i ilorazie 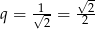 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
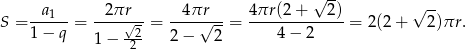
Odpowiedź: