/Szkoła średnia/Ciągi/Szereg geometryczny

Zadanie nr 2788878

Dodaj do ulubionych
Dodaj do rozwiązanych

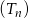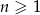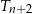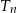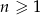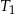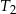Na płaszczyźnie dany jest nieskończony ciąg (Tn) , dla n ≥ 1 , trójkątów równobocznych. Pole trójkąta Tn+2 jest dwa razy mniejsze od pola trójkąta Tn dla n ≥ 1 . Uzasadnij, że suma pól trójkątów T1 i T 2 jest równa sumie pól wszystkich pozostałych trójkątów.

Rozwiązanie

Jeżeli oznaczymy przez 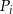Pi pole trójkąta 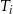Ti , to wiemy, że

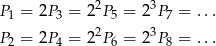
2 3 P1 = 2P 3 = 2 P5 = 2 P7 = ... P2 = 2P 4 = 22P6 = 2 3P8 = ...

Sposób I

Wiemy, że ciąg

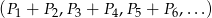
(P 1 + P 2,P3 + P4,P5 + P6,...)

jest ciągiem geometrycznym o ilorazie 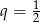1 q = 2 . Suma wszystkich wyrazów tego ciągu jest równa

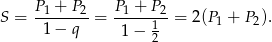
P + P P + P S = -1----2-= -1----2-= 2(P1 + P2). 1 − q 1 − 12

W takim razie suma pól trójkątów 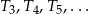T3,T4,T5,... jest równa

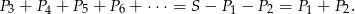
P3 + P4 + P5 + P6 + ⋅⋅⋅ = S − P1 − P2 = P 1 + P 2.

Sposób II

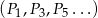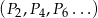Wiemy, że ciągi (P1,P 3,P 5...) i (P2,P4,P6 ...) są ciągami geometrycznymi o ilorazie 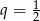q = 1 2 , więc ich sumy są odpowiednio równe

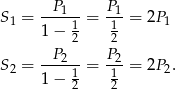
-P1--- P-1 S1 = 1− 1 = 1 = 2P 1 2 2 -P2--- P-2 S2 = 1− 1 = 1 = 2P 2. 2 2

W takim razie suma pól trójkątów 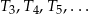T3,T4,T5,... jest równa

(P1+ P3+ P 5+ ⋅⋅⋅) + (P2+ P4+ P 6+ ⋅⋅⋅) − P1 − P2 = S1 + S2 − P1− P2 = P1 + P2.
Wersja PDF