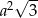Zadanie nr 3129473
Niech 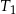 będzie trójkątem równobocznym o boku długości
będzie trójkątem równobocznym o boku długości  . Konstruujemy kolejno trójkąty równoboczne
. Konstruujemy kolejno trójkąty równoboczne 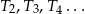 takie, że bok kolejnego trójkąta jest równy wysokości poprzedniego trójkąta. Oblicz sumę pól wszystkich tak utworzonych trójkątów
takie, że bok kolejnego trójkąta jest równy wysokości poprzedniego trójkąta. Oblicz sumę pól wszystkich tak utworzonych trójkątów 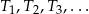 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
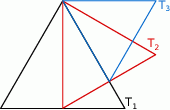
Ze wzoru 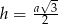 na wysokość w trójkącie równobocznym o boku
na wysokość w trójkącie równobocznym o boku  , wiemy, że długości boków kolejnych trójkątów tworzą ciąg geometryczny o pierwszym wyrazie
, wiemy, że długości boków kolejnych trójkątów tworzą ciąg geometryczny o pierwszym wyrazie  i ilorazie
i ilorazie 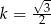 . Ponieważ stosunek pól trójkątów podobnych jest równy kwadratowi skali podobieństwa, pola trójkątów
. Ponieważ stosunek pól trójkątów podobnych jest równy kwadratowi skali podobieństwa, pola trójkątów 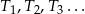 tworzą ciąg geometryczny
tworzą ciąg geometryczny 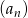 o pierwszym wyrazie
o pierwszym wyrazie 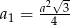 i ilorazie
i ilorazie 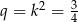 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
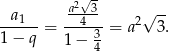
Odpowiedź: