Zadanie nr 3760113

Ciąg 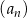(an) jest określony dla 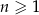n ≥ 1 i spełnia warunki

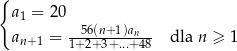
{ a1 = 2 0 an+ 1 = --56(n+-1)an-- dla n ≥ 1 1+2+ 3+...+ 48

Oblicz granicę

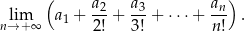
( ) lim a + a2+ a3-+ ⋅⋅⋅+ an- . n→ +∞ 1 2! 3! n!

Rozwiązanie

Ze wzoru na sumę kolejnych wyrazów ciągu arytmetycznego

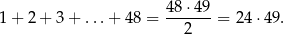
48 ⋅49 1 + 2 + 3 + ...+ 48 = -------= 24 ⋅49. 2

Zatem

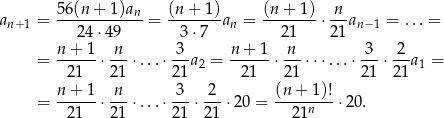
56 (n + 1)an (n+ 1) (n+ 1) n an+ 1 = ------------ = -------an = --------⋅--an −1 = ...= 24 ⋅49 3 ⋅7 21 21 = n-+-1-⋅ n--⋅...⋅-3-a2 = n-+-1-⋅-n-⋅⋅ ⋅...⋅-3-⋅-2-a1 = 21 21 21 21 2 1 21 2 1 n + 1 n 3 2 (n + 1 )! = --21--⋅ 21-⋅...⋅21-⋅ 21 ⋅ 20 =---21n-- ⋅20.

Zatem

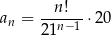
n! an = --n−-1 ⋅2 0 21

i interesująca nas granica jest równa

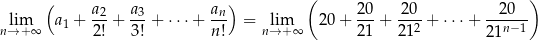
( a 2 a3 an) ( 20 20 2 0 ) lim a1 + ---+ ---+ ⋅⋅⋅+ --- = lim 20+ ---+ --2 + ⋅⋅⋅+ --n−1- n→ +∞ 2! 3! n! n→ +∞ 21 21 21

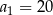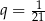Jest to więc suma wszystkich wyrazów nieskończonego ciągu geometrycznego, w którym a1 = 20 i 1- q = 21 . Suma ta jest równa

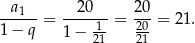
a1 20 20 ------= -----1-= 20-= 21. 1− q 1 − 21 21

Odpowiedź: 21