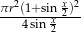Zadanie nr 4263941
W kąt o mierze  wpisano ciąg kół w taki sposób, że pierwsze koło ma promień
wpisano ciąg kół w taki sposób, że pierwsze koło ma promień  i jest styczne do ramion kąta a każde następne koło ma mniejszy promień i jest styczne do poprzedniego koła oraz do ramion kąta. Oblicz sumę pól kół tego ciągu.
i jest styczne do ramion kąta a każde następne koło ma mniejszy promień i jest styczne do poprzedniego koła oraz do ramion kąta. Oblicz sumę pól kół tego ciągu.
Rozwiązanie
Ponieważ mamy obliczyć nieskończoną sumę i w szkole nie sumuje się innych szeregów niż geometryczne, to możemy siedomyślać, że promienie danych okręgów będą tworzyć malejący ciąg geometryczny. Pozostało znaleźć jego iloraz.
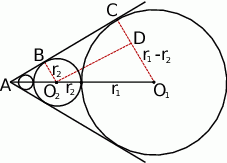
Na rysunku mamy narysowane dwa kolejne koła, musimy wyliczyć 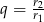 . Można to zrobić na różne sposoby, my obliczymy to z trójkąta prostokątnego
. Można to zrobić na różne sposoby, my obliczymy to z trójkąta prostokątnego 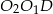 (którego kąt ostry jest równy
(którego kąt ostry jest równy 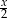 ). Mamy
). Mamy
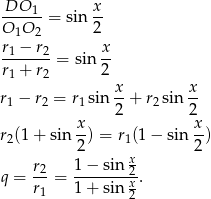
Możemy więc obliczyć sumę 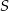 pól wszystkich okręgów
pól wszystkich okręgów
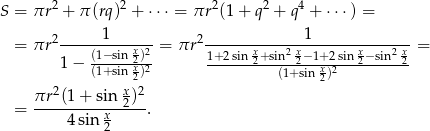
Odpowiedź: