/Szkoła średnia/Ciągi/Szereg geometryczny

Zadanie nr 5539716

Dodaj do ulubionych
Dodaj do rozwiązanych

Wartości funkcji 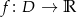f : D → R spełniają dla każdego 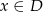x ∈ D następujące równanie

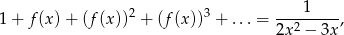
1 + f (x)+ (f(x))2 + (f(x))3 + ...= ----1----, 2x 2 − 3x

gdzie lewa strona równania jest sumą szeregu geometrycznego.

  • Wyznacz dziedzinę i wzór funkcji f .
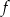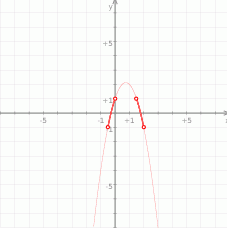
  • Naszkicuj wykres funkcji f .

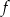Rozwiązanie

  • Wyznaczmy najpierw wzór funkcji 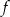f . Ze wzoru na sumę szeregu geometrycznego, mamy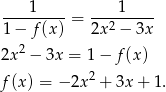
    ----1---- ---1----- 1 − f (x) = 2x2 − 3x 2x 2 − 3x = 1 − f(x) 2 f (x ) = − 2x + 3x + 1.

    Aby szereg był zbieżny musi być spełniona nierówność 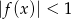|f (x)| < 1 , czyli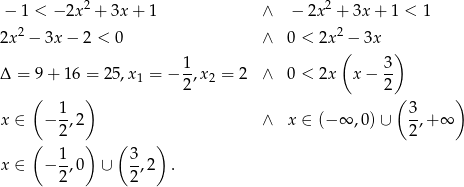

    2 2 − 1 < − 2x + 3x + 1 ∧ − 2x + 3x + 1 < 1 2x2 − 3x − 2 < 0 ∧ 0 < 2x 2 − 3x ( ) Δ = 9 + 1 6 = 25,x = − 1,x = 2 ∧ 0 < 2x x− 3- 1 2 2 2 ( 1 ) ( 3 ) x ∈ − -,2 ∧ x ∈ (− ∞ ,0)∪ -,+ ∞ ( 2 ) ( ) 2 1 3 x ∈ − -,0 ∪ --,2 . 2 2

     
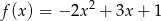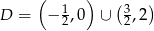
    Odpowiedź: 2 f(x ) = − 2x + 3x + 1 , ( 1 ) (3 ) D = − 2 ,0 ∪ 2,2

  • Wykres rysujemy bez trudu.
    PIC
Wersja PDF