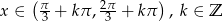/Szkoła średnia/Ciągi/Szereg geometryczny

Zadanie nr 6274480

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz te wartości x , dla których istnieje suma nieskończonego ciągu geometrycznego

1, 2cos x, 4 cos2 x, ...

Rozwiązanie

Będziemy korzystać z faktu, że szereg geometryczny

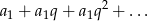
2 a1 + a1q+ a1q + ...

jest zbieżny wtedy i tylko wtedy gdy 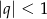|q| < 1 . Iloraz danego ciągu geometrycznego wynosi 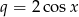q = 2co sx . Musimy zatem rozwiązać nierówność

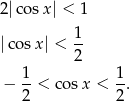
2|co sx| < 1 1 |cos x| < -- 2 − 1-< cosx < 1. 2 2

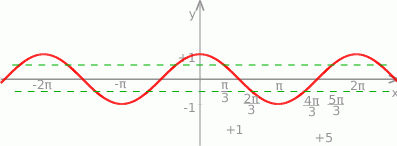
Rozwiązanie tej nierówności możemy odczytać z wykresu: 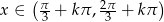(π 2π ) x ∈ -3 + kπ, 3-+ kπ .

PIC

 
Odpowiedź: ( ) x ∈ π3-+ kπ , 23π-+ kπ , k ∈ Z

Wersja PDF