/Szkoła średnia/Ciągi/Szereg geometryczny

Zadanie nr 6313003

Dodaj do ulubionych
Dodaj do rozwiązanych

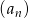Ciąg (an) jest określony dla 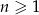n ≥ 1 i spełnia warunek

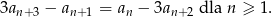
3an +3 − an+1 = an − 3an +2 dla n ≥ 1.

Oblicz sumę dwóch początkowych wyrazów ciągu 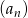(an) jeżeli suma wszystkich jego wyrazów jest równa 2016.

Rozwiązanie

Zapiszmy dany warunek w postaci

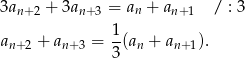
3a + 3a = a + a / : 3 n+ 2 n+3 n n+1 1- an+ 2 + an+3 = 3 (an + an+1).

Warunek ten oznacza, że ciąg

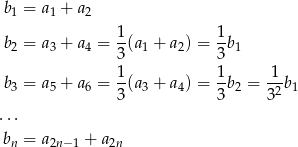
b1 = a1 + a2 1 1 b2 = a3 + a4 = -(a1 + a2) = --b1 3 3 b3 = a5 + a6 = 1(a3 + a ) = 1-b2 = -1b 3 4 3 32 1 ... bn = a2n− 1 + a 2n

jest ciągiem geometrycznym o ilorazie 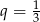1 q = 3 . Suma wszystkich wyrazów ciągu 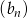(bn) jest dokładnie taka sama jak suma wszystkich wyrazów ciągu 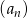(an) , więc korzystając ze wzoru na sumę szeregu geometrycznego mamy

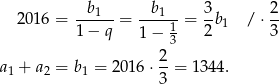
b1 b 1 3 2 201 6 = 1-−-q-= ----1-= 2b1 / ⋅ 3- 1− 3 2- a1 + a2 = b1 = 201 6⋅ 3 = 134 4.

 
Odpowiedź: a + a = 134 4 1 2

Wersja PDF