/Szkoła średnia/Ciągi/Szereg geometryczny

Zadanie nr 6583284

Dany jest nieskończony ciąg okręgów 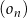(on) o równaniach 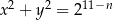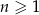2 2 11−n x + y = 2 , n ≥ 1 . Niech 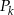Pk będzie pierścieniem ograniczonym zewnętrznym okręgiem 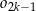o2k−1 i wewnętrznym okręgiem 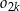o2k . Oblicz sumę pól wszystkich pierścieni 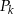P k , gdzie k ≥ 1 .

Wersja PDF

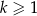Rozwiązanie

Szkicujemy opisaną sytuację – okrąg 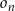on jest okręgiem o środku 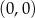(0 ,0) i promieniu √ ------ 2 11−n .

PIC

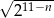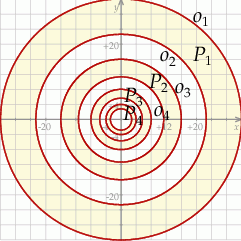
Pole pierwszego pierścienia kołowego jest równe

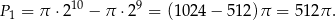
P1 = π ⋅ 210 − π ⋅ 29 = (1024 − 512 )π = 5 12π .

Pole każdego kolejnego pierścienia kołowego jest cztery razy mniejsze (bo promienie ograniczających go okręgów są 2 razy mniejsze). Mamy więc do czynienia z szeregiem geometrycznym o pierwszym wyrazie 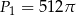P = 512π 1 i ilorazie 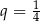1 q = 4 . Suma tego szeregu jest równa

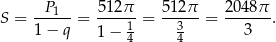
P1 5 12π 51 2π 2048 π S = ------= -----1= --3---= ------. 1− q 1 − 4 4 3

 
Odpowiedź: 2048π 3

Wersja PDF