/Szkoła średnia/Ciągi/Szereg geometryczny

Zadanie nr 7083870

Dodaj do ulubionych
Dodaj do rozwiązanych

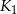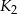W kwadrat K 1 o boku a wpisujemy kwadrat K2 , którego wierzchołki są środkami boków kwadratu 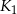K 1 , następnie w kwadrat 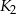K 2 wpisujemy kwadrat 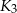K 3 , którego wierzchołki są środkami boków 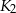K 2 i tak dalej. Oblicz sumę pól otrzymanego w ten sposób nieskończonego ciągu kwadratów.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

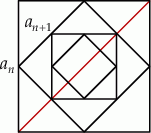
Jeżeli 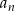an jest długością boku n –tego kwadratu, to

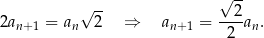
√ -- 2a = a √ 2- ⇒ a = --2a . n+1 n n+ 1 2 n

Zatem pola tych kwadratów spełniają

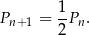
Pn+1 = 1Pn . 2

Musimy więc wysumować szereg geometryczny o pierwszym wyrazie 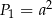P 1 = a2 i ilorazie q = 12 .

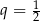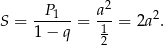
2 S = --P1--= a--= 2a2. 1 − q 1 2

 
Odpowiedź: 2 2a

Wersja PDF