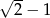/Szkoła średnia/Ciągi/Szereg geometryczny

Zadanie nr 7854765

Dodaj do ulubionych
Dodaj do rozwiązanych

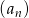Ciąg (an) jest określony dla 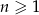n ≥ 1 i spełnia warunki

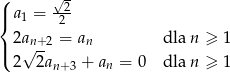
( √2- |{ a1 = 2 2an+ 2 = an dla n ≥ 1 |( √ -- 2 2an +3 + an = 0 dla n ≥ 1

Oblicz granicę

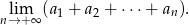
lim (a1 + a2 + ⋅ ⋅⋅+ an). n→ +∞

Rozwiązanie

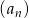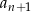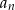Spróbujemy z podanego warunku definiującego ciąg (an) uzyskać zależność an+ 1 od an . Podstawmy w drugim z warunków 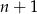n+ 1 zamiast n . Mamy wtedy

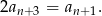
2an+ 3 = an+1.

Używamy teraz tej zależności w trzecim warunku

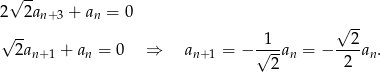
√ -- 2 2an+ 3 + an = 0 √ -- √ 2a + a = 0 ⇒ a = − √1-a = − --2a . n+ 1 n n+ 1 2 n 2 n

To oznacza, że ciąg 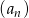(an) jest ciągiem geometrycznym o ilorazie 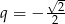√ - q = − --2 2 i interesująca nas granica to suma wyznaczonego przez ten ciąg szeregu geometrycznego. Suma tego szeregu jest równa

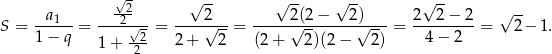
√-2 √ -- √ -- √ -- √ -- S = -a1--= ---2√-- = ----2√---= -----2√-(2−----2√)---= 2--2-−-2-= √ 2− 1. 1− q 1 + --2 2+ 2 (2 + 2 )(2 − 2 ) 4− 2 2

 
Odpowiedź: √ -- 2 − 1

Wersja PDF