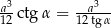/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy trójkątny/Przekroje

Zadanie nr 4748686

Dodaj do ulubionych
Dodaj do rozwiązanych

Ostrosłup prawidłowy trójkątny przecięto płaszczyzną, która przechodzi przez krawędź podstawy długości a oraz jest prostopadła do przeciwległej krawędzi bocznej. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem α . Oblicz objętość ostrosłupa.

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

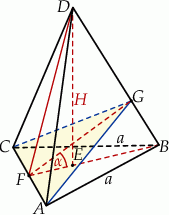
Ponieważ znamy długość krawędzi podstawy, do wyliczenia objętości brakuje nam wysokości 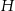H . Oznaczmy wysokość podstawy przez √- h = a-3- 2 .

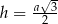Sposób I

Wiemy, że płaszczyzna 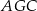AGC jest prostopadła do krawędzi 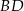BD , więc trójkąt 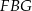F BG jest prostokątny. W szczególności 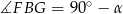∘ ∡F BG = 9 0 − α . W trójkącie 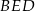BED mamy

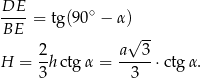
DE ---- = tg(90∘ − α) BE √ -- 2- a---3 H = 3 hctg α = 3 ⋅ ctg α.

Pozostało obliczyć objętość

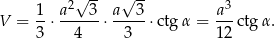
√ -- √ -- 1- a2--3- a--3- a3- V = 3 ⋅ 4 ⋅ 3 ⋅ctgα = 12 ctgα.

Sposób II

Tym razem wysokość 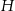H obliczymy licząc na dwa sposoby pole trójkąta 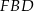FBD . Mamy

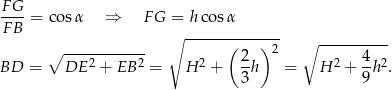
F-G- F B = cosα ⇒ FG = h cosα ∘ ------(----)2 ∘ ---------- ∘ ---2------2- 2 2- 2 4-2 BD = DE + EB = H + 3 h = H + 9h .

Liczymy teraz pole trójkąta 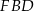FBD na dwa sposoby.

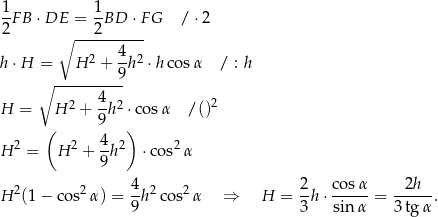
1 1 2F B ⋅DE = 2BD ⋅F G /⋅ 2 ∘ ---------- h⋅ H = H 2 + 4h 2 ⋅h cosα / : h 9 ∘ ---------- H = H 2 + 4-h2 ⋅co sα /()2 ( 9 ) 2 2 4 2 2 H = H + 9h ⋅ cos α H 2(1− cos2α ) = 4h2 cos2α ⇒ H = 2-h⋅ cosα-= --2h--. 9 3 sin α 3 tg α

Podstawmy w tej równości 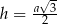a√-3- h = 2 .

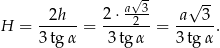
a√3 √ -- --2h-- 2-⋅-2-- -a--3- H = 3 tg α = 3tg α = 3 tg α .

Pozostało obliczyć objętość.

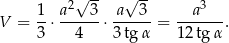
2√ -- √ -- 3 V = 1-⋅ a---3⋅ a--3--= --a---. 3 4 3tg α 12tg α

 
Odpowiedź: a3 ctg α = -a3-- 12 12tg α

Wersja PDF