Zadanie nr 5907032
Wysokość ostrosłupa prawidłowego trójkątnego jest równa 4, a krawędź podstawy ma długość 1. Ostrosłup przecięto płaszczyzną, która przechodzi przez krawędź podstawy oraz jest prostopadła do przeciwległej krawędzi bocznej. Oblicz pole powierzchni tego przekroju.
Rozwiązanie
Rozpoczynamy od rysunku.
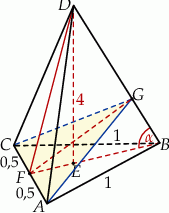
Ponieważ znamy długość krawędzi podstawy, do obliczenia pola przekroju brakuje nam wysokości 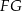 tego przekroju.
tego przekroju.
Zauważmy najpierw, że
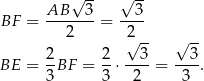
Wiemy, że płaszczyzna 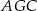 jest prostopadła do krawędzi
jest prostopadła do krawędzi 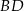 , więc trójkąt
, więc trójkąt 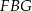 jest prostokątny. Trójkąt ten ma kąt wspólny
jest prostokątny. Trójkąt ten ma kąt wspólny 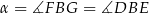 z trójkątem prostokątnym
z trójkątem prostokątnym 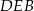 .
.
Sposób I
W trójkątach 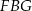 i
i 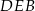 mamy
mamy
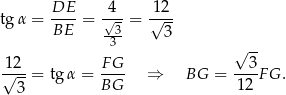
Piszemy teraz twierdzenie Pitagorasa w trójkącie 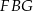 .
.
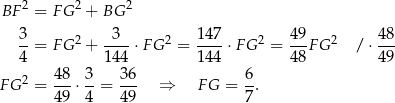
Pole trójkąta 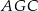 jest więc równe
jest więc równe
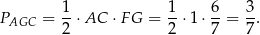
Sposób II
Jak już zauważyliśmy, trójkąty prostokątne 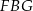 i
i 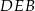 mają wspólny kąt ostry, więc są podobne. W szczególności,
mają wspólny kąt ostry, więc są podobne. W szczególności,
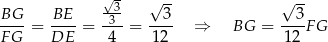
Dalej postępujemy tak samo jak w sposobie I.
Sposób III
Tym razem liczymy pole trójkąta 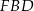 na dwa sposoby. Zanim jednak to zrobimy, obliczmy długość krawędzi bocznej
na dwa sposoby. Zanim jednak to zrobimy, obliczmy długość krawędzi bocznej
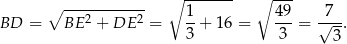
Zgodnie z zapowiedzią, liczymy teraz pole trójkąta 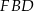 na dwa sposoby.
na dwa sposoby.
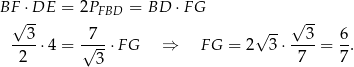
Pole trójkąta 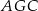 jest więc równe
jest więc równe
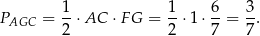
Odpowiedź: