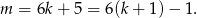Zadanie nr 2590108
Wykaż, że każda liczba pierwsza większa od 3 jest postaci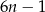 
lub 
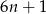dla pewnej liczby naturalnej 
.
Rozwiązanie
Każdą liczbę naturalną możemy zapisać w postaci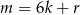 
, gdzie 
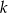jest pewną liczbą całkowitą, a 
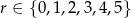jest resztą z dzielenia liczby 
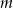przez 6. Zauważmy, że jeżeli 
jest jedną z liczb: 0,2,4 to
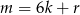
jest liczbą parzystą, więc nie może być liczbą pierwszą większą od 3. Podobnie, jeżeli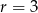 
to 
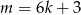jest liczbą podzielną przez 3. To oznacza, że dla liczby pierwszej 
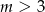musi być 
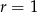lub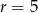 
. W tym drugim przypadku liczbę 
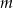możemy zapisać w postaci
