/Szkoła średnia/Liczby/Liczby całkowite/Reszty

Zadanie nr 2709884

Dodaj do ulubionych
Dodaj do rozwiązanych

Udowodnij, że każda liczba całkowita 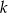k , która przy dzieleniu przez 7 daje resztę 2, ma tę własność, że reszta z dzielenia liczby 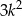3k 2 przez 7 jest równa 5.

Rozwiązanie

Jeżeli liczba 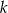k daje resztę 2 przy dzieleniu przez 7, to jest postaci 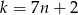k = 7n+ 2 . wtedy

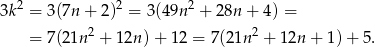
2 2 2 3k = 3(7n + 2) = 3(4 9n + 28n + 4) = = 7(21n2 + 12n )+ 12 = 7(21n 2 + 12n + 1) + 5.

Widać teraz, że liczba 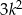2 3k daje resztę 5 przy dzieleniu przez 7.

Wersja PDF