Zadanie nr 3286230
Wykaż, że reszta z dzielenia sumy kwadratów czterech kolejnych nieparzystych liczb naturalnych przez 16 jest równa 4.
Rozwiązanie
Oznaczmy przez 
dowolną liczbę naturalną. Wówczas czterema kolejnymi liczbami naturalnymi nieparzystymi będą
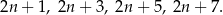
Obliczmy ile wynosi suma kwadratów tych liczb
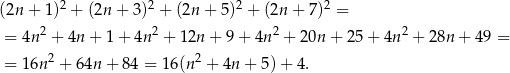
Widać teraz, że liczba ta daje resztę 4 przy dzieleniu przez 16.
