/Szkoła średnia/Liczby/Liczby całkowite/Reszty

Zadanie nr 6157650

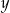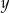Reszta z dzielenia liczby x przez 4 jest równa 3. Reszta z dzielenia liczby y przez 4 jest równa 1. Wykaż, że różnica kwadratów liczb x i y jest podzielna przez 4.

Wersja PDF

Rozwiązanie

Na mocy podanych informacji możemy przyjąć, że 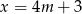x = 4m + 3 i y = 4n + 1 .

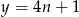Sposób I

Korzystamy ze wzoru skróconego mnożenia na kwadrat sumy.

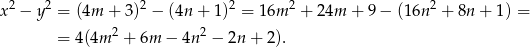
x2 − y2 = (4m + 3)2 − (4n + 1)2 = 16m 2 + 24m + 9 − (16n 2 + 8n + 1) = = 4(4m 2 + 6m − 4n2 − 2n + 2).

Widać teraz, że liczba ta rzeczywiście dzieli się przez 4.

Sposób II

Korzystamy ze wzoru skróconego mnożenia różnicę kwadratów.

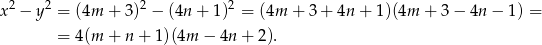
x2 − y2 = (4m + 3)2 − (4n + 1)2 = (4m + 3 + 4n + 1)(4m + 3 − 4n − 1 ) = = 4(m + n + 1)(4m − 4n + 2).

Widać teraz, że liczba ta rzeczywiście dzieli się przez 4.

Wersja PDF