Zadanie nr 7295891
Wykaż, że suma kwadratów trzech liczb całkowitych, które przy dzieleniu przez 3 dają resztę 2 jest podzielna przez 3.
Rozwiązanie
Niech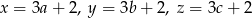 
będą trzema liczbami, które przy dzieleniu przez 3 dają resztę 2. Mamy wtedy
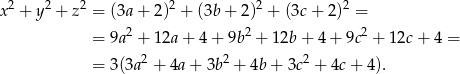
Widać teraz, że liczba ta rzeczywiście dzieli się przez 3.
