Zadanie nr 9140319
Uzasadnij, że jeżeli liczba całkowita  nie dzieli się przez 5, to
nie dzieli się przez 5, to 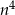 daje przy dzieleniu przez 5 resztę 1.
daje przy dzieleniu przez 5 resztę 1.
Rozwiązanie
Sposób I
Jeżeli liczba całkowita nie dzieli się przez 5, to jest postaci 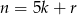 , gdzie
, gdzie  jest jedną z liczb: 1, 2, 3, 4. W takim razie
jest jedną z liczb: 1, 2, 3, 4. W takim razie
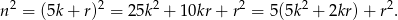
Podstawiając teraz każdą z 4 możliwych wartości  zauważmy, że liczba
zauważmy, że liczba 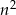 zawsze daje resztę 1 lub 4 przy dzieleniu przez 5, więc jest postaci
zawsze daje resztę 1 lub 4 przy dzieleniu przez 5, więc jest postaci 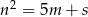 , gdzie
, gdzie 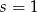 lub
lub 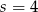 . Stąd
. Stąd
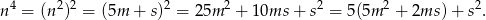
Podstawiając teraz 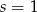 i
i 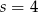 sprawdzamy, że liczba
sprawdzamy, że liczba 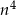 w obu przypadkach daje resztę 1 przy dzieleniu przez 5.
w obu przypadkach daje resztę 1 przy dzieleniu przez 5.
Sposób II
Zauważmy, że wystarczy wykazać, że liczba 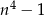 jest podzielna przez 5. Zauważmy, że
jest podzielna przez 5. Zauważmy, że
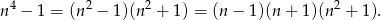
Wystarczy zatem udowodnić, że jedna z liczb: 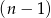 ,
, 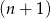 lub
lub 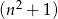 jest podzielna przez 5. Aby to zrobić załóżmy, że pierwsze dwie liczby nie dzielą się przez 5 – pokażemy, że w takiej sytuacji trzecia liczba musi dzielić się przez 5. Jeżeli żadna z liczb
jest podzielna przez 5. Aby to zrobić załóżmy, że pierwsze dwie liczby nie dzielą się przez 5 – pokażemy, że w takiej sytuacji trzecia liczba musi dzielić się przez 5. Jeżeli żadna z liczb 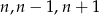 nie dzieli się przez 5, to
nie dzieli się przez 5, to  musi być postaci
musi być postaci 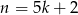 lub
lub 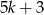 . Mamy wtedy odpowiednio
. Mamy wtedy odpowiednio
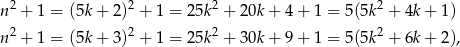
Zatem rzeczywiście 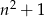 dzieli się przez 5.
dzieli się przez 5.

